در این راهنما یاد میگیرید مخرج مشترک چیست، چرا در جمع/تفریق و مقایسهٔ کسرها ضروری است و چطور با دو روش سریع (ضرب مخرجها و ک.م.م) آن را پیدا کنید. برای هر روش مثال حلشده و در پایان آزمون کوتاه هم دارید.
مخرج مشترک چیست؟
هر کسر از صورت (بالا) و مخرج (پایین) تشکیل میشود. وقتی مخرجهای دو یا چند کسر برابر باشند، آن مقدارِ برابر را
مخرج مشترک مینامیم. یکسان شدن مخرجها شرط اصلی برای جمع، تفریق و مقایسهٔ کسرهاست.
چگونه مخرج مشترک بگیریم؟ (نمای کلی)
- روش ۱: ضرب مخرجها – برای دو کسر، صورت و مخرج هر کسر را در مخرجِ کسر دیگر ضرب کنید؛ مخرج جدید برابر حاصلضرب دو مخرج است.
- روش ۲: ک.م.م – کوچکترین مضرب مشترک مخرجها را بیابید (با لیست مضربها یا تجزیه به عوامل اوّل) و کسرها را به آن تبدیل کنید. این روش معمولاً
مخرج کوچکتری میدهد و حساب را سادهتر میکند.
روش اول: ضرب مخرجها
مثال ۱ – مقایسهٔ دو کسر
کدام بزرگتر است؟ ۱/۵ یا ۲/۷
- مخرج مشترک = ۵ × ۷ = ۳۵
- ۱/۵ ←
۱×۷ / ۵×۷ = ۷/۳۵ - ۲/۷ ←
۲×۵ / ۷×۵ = ۱۰/۳۵
نتیجه: چون ۱۰/۳۵ > ۷/۳۵ پس ۲/۷ بزرگتر است.
مثال ۲ – جمع دو کسر با مخرج نامساوی
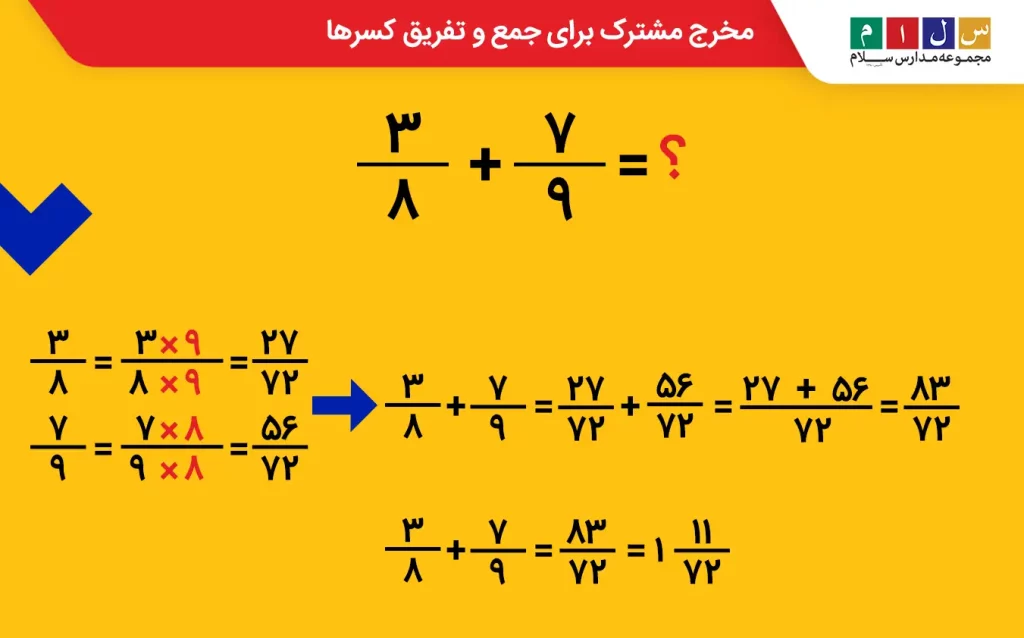
- مخرج مشترک = ۸ × ۹ = ۷۲
- ۳/۸ ← ۲۷/۷۲ ، ۷/۹ ← ۵۶/۷۲
- جمع:
۲۷/۷۲ + ۵۶/۷۲ = ۸۳/۷۲ = ۱ و ۱۱/۷۲
روش دوم: ک.م.م (کوچکترین مضرب مشترک)
برای یافتن ک.م.مِ دو مخرج میتوانید:
- مضربها را فهرست کنید: کوچکترین مضربی که در هر دو فهرست مشترک است، ک.م.م است.
- به عاملهای اوّل تجزیه کنید: حاصلضربِ عاملهای مشترک با بیشترین توان × عاملهای غیراشتراک، ک.م.م را میدهد.
مثال – تفریق با ک.م.م
۵/۱۲ − ۱/۱۸
- ۱۲ = ۲² × ۳ و ۱۸ = ۲ × ۳² ⇒ ک.م.م = ۲² × ۳² = ۳۶
- ۵/۱۲ ← ۱۵/۳۶ ، ۱/۱۸ ← ۲/۳۶
- تفریق:
۱۵/۳۶ − ۲/۳۶ = ۱۳/۳۶
مخرج مشترک بین سه کسر
برای چند کسر، ک.م.مِ همهٔ مخرجها را بگیرید. مثال: مخرجها ۸، ۶ و ۹ ⇒ تجزیه: ۸ = ۲³، ۶ = ۲×۳، ۹ = ۳² ⇒ ک.م.م = ۲³ × ۳² = ۷۲.
نمونهٔ حل:
۵/۸ + ۱/۶ − ۱/۹
- مخرج مشترک = ۷۲
- ۵/۸ = ۴۵/۷۲ ، ۱/۶ = ۱۲/۷۲ ، ۱/۹ = ۸/۷۲
- نتیجه:
۴۵/۷۲ + ۱۲/۷۲ − ۸/۷۲ = ۴۹/۷۲
آزمون سنجش یادگیری
سوال ۱
کدام گزینه میتواند مخرج مشترکِ ۱/۱۶ و ۳/۸ باشد؟
- ۲۴
- ۱۸
- ۱۶
- ۴۰
پاسخ تشریحی
مضربهای ۸: ۸، ۱۶، ۲۴، ۳۲… و مضربهای ۱۶: ۱۶، ۳۲، ۴۸… کوچکترین مضرب مشترک = ۱۶.
سوال ۲
حاصل ۲/۳ − ۱/۷ کدام است؟
- ۱۱/۲۱
- ۵/۲۱
- ۱۳/۲۱
- ۸/۲۱
پاسخ تشریحی
ک.م.م(۳,۷)=۲۱ ⇒ ۲/۳=۱۴/۲۱ و ۱/۷=۳/۲۱ ⇒ ۱۴/۲۱−۳/۲۱=۱۱/۲۱.
سوال ۳
حاصل ۲ + ۱۶/۵ برابر است با؟
- ۲۱/۵
- ۲۳/۵
- ۲۶/۵
- ۲۸/۵
پاسخ تشریحی
۲ = ۱۰/۵ ⇒ ۱۰/۵ + ۱۶/۵ = ۲۶/۵.
سوال ۴
۳ ۱/۶ + ۲ ۲/۹ = ؟ (به کسر نامتعارفی بنویسید)
- ۸۷/۱۸
- ۹۷/۱۸
- ۹۱/۱۸
- ۹۵/۱۸
پاسخ تشریحی
۳ ۱/۶ = ۱۹/۶ و ۲ ۲/۹ = ۲۰/۹ ⇒ ک.م.م(۶,۹)=۱۸ ⇒ ۱۹/۶=۵۷/۱۸ و ۲۰/۹=۴۰/۱۸ ⇒ جمع: ۹۷/۱۸ = ۵ و ۷/۱۸.
جمعبندی نکات کلیدی
- برای جمع، تفریق و مقایسهٔ کسرها، ابتدا مخرجها را یکسان کنید.
- ضرب مخرجها سریع و ساده است، اما همیشه کوچکترین مخرج را نمیدهد.
- ک.م.م معمولاً بهترین گزینه برای مخرج مشترکِ کوچکتر و محاسبات تمیزتر است.
- هر عددی را که در مخرج ضرب میکنید، همان را در صورت هم ضرب کنید تا مقدار کسر ثابت بماند.
سوالات متداول
۱) مخرج مشترک چیست؟
مقداری که مخرج چند کسر را یکسان میکند تا بتوان آنها را جمع/تفریق یا با هم مقایسه کرد.
۲) چه زمانی از ک.م.م استفاده کنیم؟
وقتی میخواهید کوچکترین مخرج ممکن را داشته باشید (بهخصوص برای چند کسر). این کار سادهسازی و اختصار را سادهتر میکند.
۳) آیا همیشه باید کوچکترین مخرج را بگیریم؟
اجباری نیست، اما توصیه میشود. هر مخرج مشترکی معتبر است؛ کوچکترین آن فقط محاسبه را آسانتر میکند.
۴) فرق روش ضرب مخرجها با ک.م.م چیست؟
در ضرب مخرجها، مخرج جدید حاصلضربِ دو مخرج است؛ در ک.م.م، از کوچکترین مضرب مشترک استفاده میکنیم که غالباً کوچکتر است.